Minimum Spanning Tree

Published on 14 October 2019 (Updated: 26 February 2024)
Minimum Spanning Tree

Welcome to the Minimum Spanning Tree page! Here, you'll find a description of the project as well as a list of sample programs written in various languages.

This article was written by:

Description

A minimum spanning tree is defined as the minimum set of edges needed to connect every node in a graph without cycles. For our purposes, we're concerned with weighted undirected graphs. In other words, we want to find the minimum cost spanning tree.

For example, let's say we have the following graph:

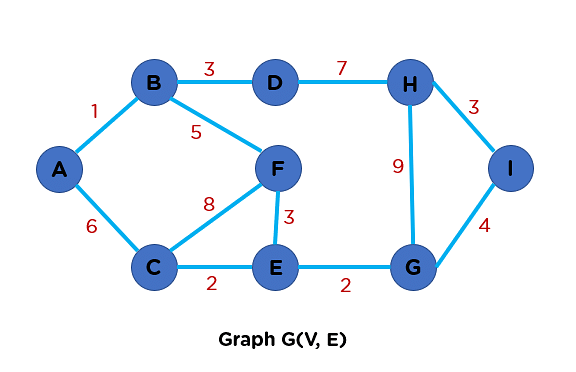
Initial Graph

Then, a possible minimum spanning tree would have the lowest total weight while also connected all nodes without cycles. Such as:

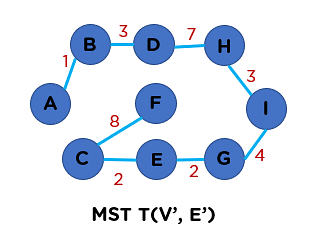
Final Graph

Naturally, there are a few ways to solve this problem, but the two most famous are Prim's algorithm and Kruskal's algorithm. Check those out before implementing this solution.

Requirements

To implement this algorithm, your program should accept a square matrix of strings in the following format:

./minimum-spanning-tree "0, 2, 0, 6, 0, 2, 0, 3, 8, 5, 0, 3, 0, 0, 7, 6, 8, 0, 0, 9, 0, 5, 7, 9, 0"

Here we've chosen to represent the matrix as a serialized list of integers. Since the input string represents a square matrix, we should be able to take the square root of the length to determine where the rows are in the string. In this case, we have 25 values, so we must have 5 nodes.

If we reformat the input string as a matrix, we'll notice that the values in the matrix represent the edge weight between each node. For example, we could reformat our example to look something like the following:

Mapping 0 1 2 3 4
0 0 2 0 6 0
1 2 0 3 8 5
2 0 3 0 0 7
3 6 8 0 0 9
4 0 5 7 9 0

Here, we can see that there is no edge between node 0 and node 2. Meanwhile, node 0 has an edge to node 3 with a weight of 6.

If we continue to look at this table, we'll notice that all the edges are mirrored across the top to bottom diagonal. In other words, the weight from node 0 to node 1 is the same as the weight from node 1 to node 0. We can use this property to differentiate between directed and undirected graphs.

For simplicity, the output sequence should print the minimum weight of the tree. In other words, what is the cost of the minimum spanning tree?

Testing

Every project in the Sample Programs repo should be tested. In this section, we specify the set of tests specific to Minimum Spanning Tree. In order to keep things simple, we split up the testing as follows:

Minimum Spanning Tree Valid Tests

Description Input Output
Sample Input: Routine "0, 2, 0, 6, 0, 2, 0, 3, 8, 5, 0, 3, 0, 0, 7, 6, 8, 0, 0, 9, 0, 5, 7, 9, 0" "16"

Minimum Spanning Tree Invalid Tests

Description Input
No Input  
Empty Input ""
Non-Square Input "1, 0, 3, 0, 5, 1"

All of these tests should output the following:

Usage: please provide a comma-separated list of integers

Articles

There are 9 articles: